Introduction
In this tutorial, we will look at various types of Keras loss functions for training neural networks. The loss functions are an important part of any neural network training process as it helps the network to minimize the error and reach as close as possible to the expected output. Here we will go through Kera loss functions for regression, classification and also see how to create a custom loss function in Keras.
What is Loss Function?
Loss Functions, also known as cost functions, are used for computing the error with the aim that the model should minimize it during training.
Loss Functions also help in finding out the slope i.e. gradient w.r.t. weights used in the model and then these weights are updated after each epoch with the help of backpropagation.
The below animation shows how a loss function works.
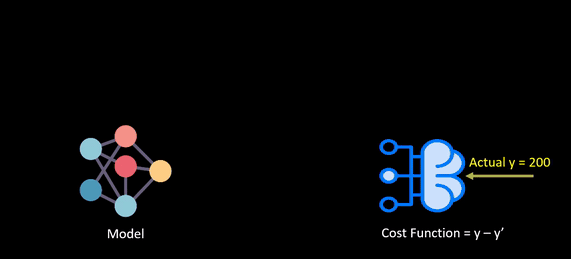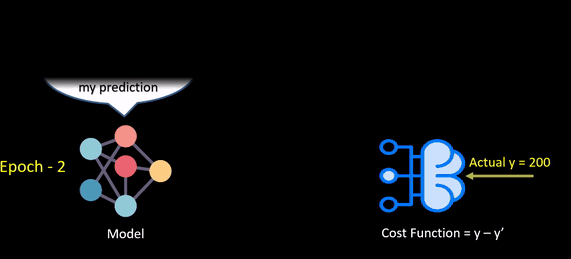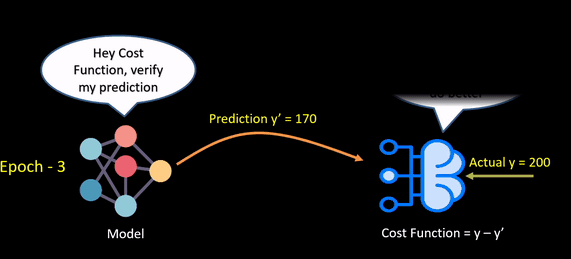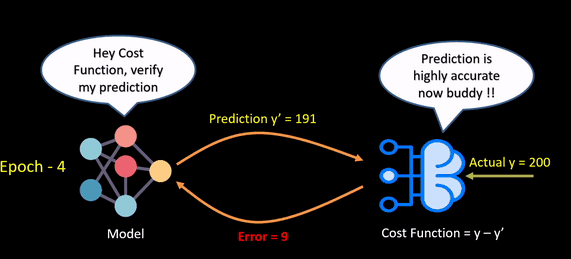
Selecting a loss function is not so easy, so we’ll be going over some prominent loss functions that can be helpful in various instances.
Types of Loss Functions in Keras
1. Keras Loss Function for Classification
Let us first understand the Keras loss functions for classification which is usually calculated by using probabilistic losses.
i) Keras Binary Cross Entropy
Binary Cross Entropy loss function finds out the loss between the true labels and predicted labels for the binary classification models that gives the output as a probability between 0 to 1.
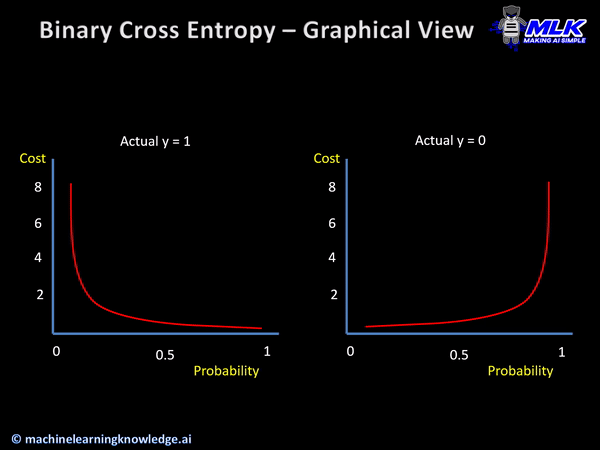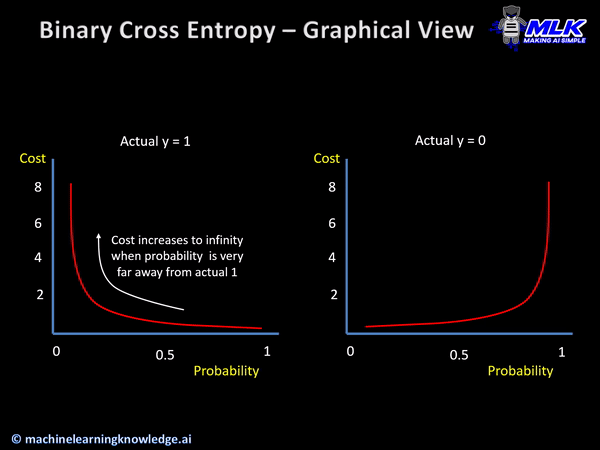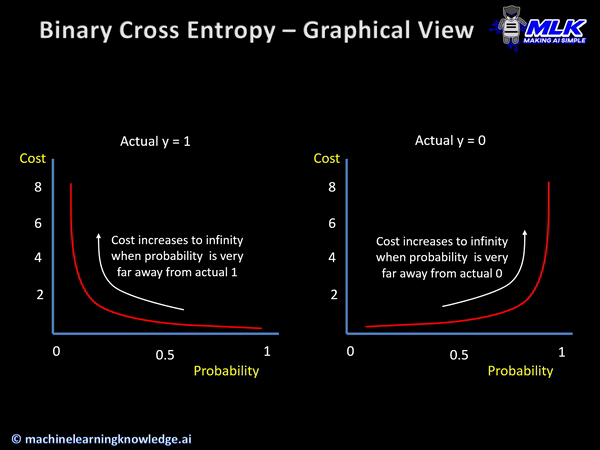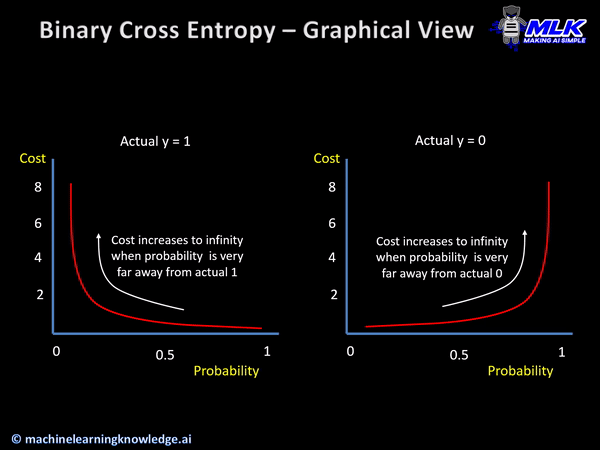
Syntax of Keras Binary Cross Entropy
Following is the syntax of Binary Cross Entropy Loss Function in Keras.
tf.keras.losses.BinaryCrossentropy(
from_logits=False, label_smoothing=0, reduction="auto", name="binary_crossentropy"
)
Keras Binary Cross Entropy Example
The example for Keras binary cross entropy shows how two sets of random values are used as data and then the required function from losses class is used.
import tensorflow as tf
y_true = [[0., 1.], [0., 0.]]
y_pred = [[0.6, 0.4], [0.4, 0.6]]
# Using 'auto'/'sum_over_batch_size' reduction type.
bce = tf.keras.losses.BinaryCrossentropy()
bce(y_true, y_pred).numpy()
ii) Keras Categorical Cross Entropy
This is the second type of probabilistic loss function for classification in Keras and is a generalized version of binary cross entropy that we discussed above. Categorical Cross Entropy is used for multiclass classification where there are more than two class labels.
Syntax of Keras Categorical Cross Entropy
Following is the syntax of Categorical Cross Entropy Loss Function in Keras.
tf.keras.losses.CategoricalCrossentropy(from_logits=False,label_smoothing=0, reduction="auto",name="categorical_crossentropy",)
Keras Categorical Cross Entropy Example
The following is an example of Keras categorical cross entropy. y_true denotes the actual probability distribution of the output and y_pred denotes the probability distribution we got from the model.
y_true = [[0, 1, 0], [0, 0, 1]]
y_pred = [[0.05, 0.95, 0], [0.1, 0.8, 0.1]]
# Using 'auto'/'sum_over_batch_size' reduction type.
cce = tf.keras.losses.CategoricalCrossentropy()
cce(y_true, y_pred).numpy()
[adrotate banner=”3″]
iii) Keras KL Divergence
Syntax of Keras KL Divergence
Below is the syntax of LL Divergence in Keras –
tf.keras.losses.KLDivergence(reduction="auto", name="kl_divergence")
Keras KL Divergence Example
The KLDivergence() function is used in this case. The result obtained shows that there is not a huge loss but still it is considerable.
y_true = [[0, 1], [0, 0]]
y_pred = [[0.6, 0.4], [0.4, 0.6]]
# Using 'auto'/'sum_over_batch_size' reduction type.
kl = tf.keras.losses.KLDivergence()
kl(y_true, y_pred).numpy()
iv) Keras Poisson Loss Function
In the Poisson loss function, we calculate the Poisson loss between the actual value and predicted value. Poisson Loss Function is generally used with datasets that consists of Poisson distribution. An example of Poisson distribution is the count of calls received by the call center in an hour.
Syntax of Keras Poisson Loss Function
Following is the syntax of Poisson Loss Function in Keras.
tf.keras.losses.Poisson(reduction="auto", name="poisson")
Keras Poisson Loss Function Example
The poisson loss function is used in below example.
y_true = [[0., 1.], [0., 0.]]
y_pred = [[1., 1.], [0., 0.]]
# Using 'auto'/'sum_over_batch_size' reduction type.
p = tf.keras.losses.Poisson()
p(y_true, y_pred).numpy()
iv) Keras Hinge Loss
The above Keras loss functions for classification were using probabilistic loss as their basis for calculation. Now we are going to see some loss functions in Keras that use Hinge Loss for maximum margin classification like in SVM.
The hinge loss function is performed by computing hinge loss of true values and predicted values.
Syntax of Keras Hinge Loss
Below is the syntax of Keras Hinge loss –
tf.keras.losses.Hinge(reduction="auto", name="hinge")
Keras Hinge Loss Example
The hinge() function from the Keras package helps in finding the hinge loss
y_true = [[0., 1.], [0., 0.]]
y_pred = [[0.6, 0.4], [0.4, 0.6]]
# Using 'auto'/'sum_over_batch_size' reduction type.
h = tf.keras.losses.Hinge()
h(y_true, y_pred).numpy()
vi) Keras Squared Hinge Loss
The squared hinge loss is calculated using squared_hinge() function and is similar to Hinge Loss calculation discussed above except that the result is squared.
Syntax of Squared Hinge Loss in Keras
tf.keras.losses.squared_hinge(y_true, y_pred)
Example of Squared Hinge Loss in Keras
In this example, at first, data is generated using numpy randon function, then Keras squared hinge loss function calculates the loss.
import numpy as np
y_true = np.random.choice([-1, 1], size=(2, 3))
y_pred = np.random.random(size=(2, 3))
loss = tf.keras.losses.squared_hinge(y_true, y_pred)
assert loss.shape == (2,)
assert np.array_equal(loss.numpy(),np.mean(np.square(np.maximum(1. - y_true * y_pred, 0.)), axis=-1))
vii) Keras Categorical Hinge Loss
The second type of hinge loss function is the categorical hinge loss function. It can help in computing categorical hinge loss between true values and predicted values for multiclass classification.
Syntax of Keras Categorical Hinge Loss
Below is the syntax of Categorical Hinge Loss in Keras –
tf.keras.losses.CategoricalHinge(reduction="auto", name="categorical_hinge")
Keras Categorical Hinge Loss Example
y_true = [[0, 1], [0, 0]]
y_pred = [[0.6, 0.4], [0.4, 0.6]]
# Using 'auto'/'sum_over_batch_size' reduction type.
h = tf.keras.losses.CategoricalHinge()
h(y_true, y_pred).numpy()
2. Keras Loss Function for Regression
Let us now see the second types of loss function in Keras for Regression models
These regression loss functions are calculated on the basis of residual or error of the actual value and predicted value. The below animation shows this concept.
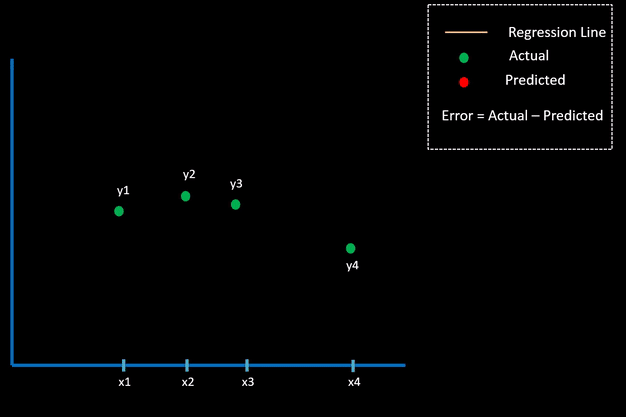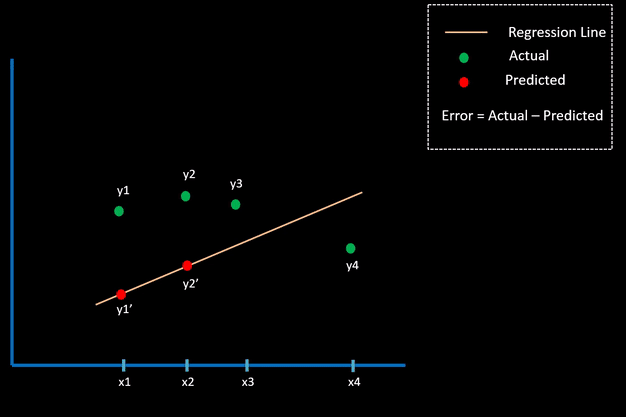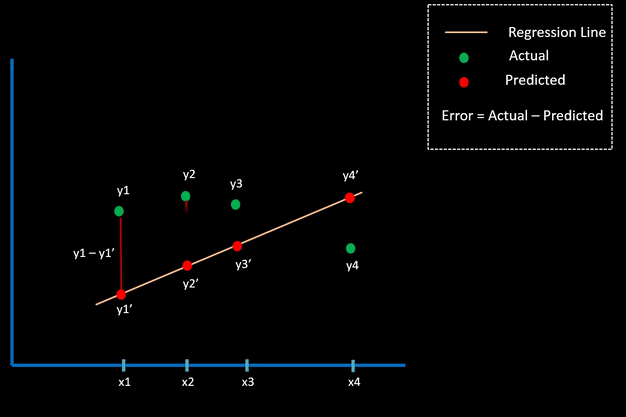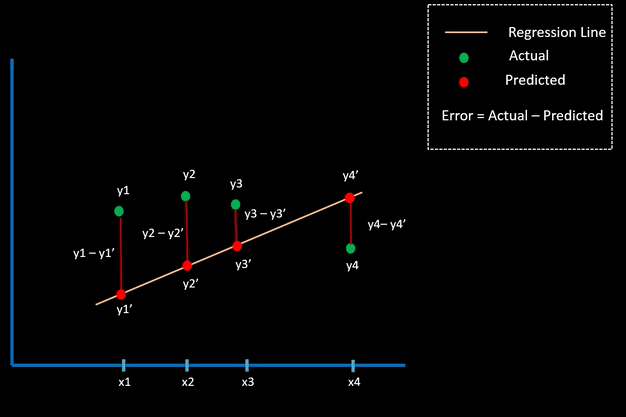
Different types of Regression Loss function in Keras are as follows:
i) Keras Mean Square Error Loss
The mean square error in Keras is used for computing the mean square of errors between predicted values and actual values to get the loss.
Syntax of Mean Square Error Loss in Keras
Below is the syntax of Keras Mean Square in Keras –
tf.keras.losses.MeanSquaredError(reduction="auto", name="mean_squared_error")
Keras Mean Square Error Loss Example
The below code snippet shows how we can implement mean square error in Keras.
y_true = [[0., 1.], [0., 0.]]
y_pred = [[1., 1.], [1., 0.]]
# Using 'auto'/'sum_over_batch_size' reduction type.
mse = tf.keras.losses.MeanSquaredError()
mse(y_true, y_pred).numpy()
ii) Keras Mean Absolute Error Loss
The mean absolute error is computed using mean of absolute difference of labels and predicted values.
Syntax of Mean Absolute Error Loss in Keras
Below is the syntax of mean absolute error loss in Keras –
tf.keras.losses.MeanAbsoluteError(
reduction="auto", name="mean_absolute_error"
)
Keras Mean Absolute Error Loss Example
With help of losses class of Keras, we can import mean absolute error and then apply this over a dataset to compute mean absolute error loss.
y_true = [[0., 1.], [0., 0.]]
y_pred = [[1., 1.], [1., 0.]]
# Using 'auto'/'sum_over_batch_size' reduction type.
mae = tf.keras.losses.MeanAbsoluteError()
mae(y_true, y_pred).numpy()
iii) Keras Cosine Similarity Loss
To calculate cosine similarity loss amongst the labels and predictions, we use cosine similarity. The value for cosine similarity ranges from -1 to 1.
Syntax of Cosine Similarity Loss in Keras
Below is the syntax of cosine similarity loss in Keras –
tf.keras.losses.CosineSimilarity(
axis=-1, reduction="auto", name="cosine_similarity"
)
Keras Cosine Similarity Loss Example
In this example, for implementing cosine similarity in Keras, we are going to use cosine_loss function.
y_true = [[0., 1.], [1., 1.]]
y_pred = [[1., 0.], [1., 1.]]
# Using 'auto'/'sum_over_batch_size' reduction type.
cosine_loss = tf.keras.losses.CosineSimilarity(axis=1)
cosine_loss(y_true, y_pred).numpy()
iv) Keras Huber Loss Function
In regression related problems where data is less affected by outliers, we can use huber loss function.
Syntax of Huber Loss Function in Keras
Below is the syntax of Huber Loss function in Keras
tf.keras.losses.Huber(delta=1.0, reduction="auto", name="huber_loss")
Huber Loss Function in Keras Example
Keras library provides Huber function for calculating the Huber loss.
y_true = [[0, 1], [0, 0]]
y_pred = [[0.6, 0.4], [0.4, 0.6]]
# Using 'auto'/'sum_over_batch_size' reduction type.
h = tf.keras.losses.Huber()
h(y_true, y_pred).numpy()
Keras Custom Loss Function
In spite of so many loss functions, there are cases when these loss functions do not serve the purpose. In such scenarios, we can build a custom loss function in Keras, which is especially useful for research purposes.
You can pass this custom loss function in Keras as a parameter while compiling the model. But there is a constraint here that the custom loss function should take the true value (y_true) and predicted value (y_pred) as input and return an array of loss. If your function does not match this signature then you cannot use this as a custom function in Keras.
Keras Custom Loss function Example
The below code snippet shows how to build a custom loss function. Once this function is created, we use it to compile the model using Keras.
def custom_loss_function(y_true, y_pred):
squared_difference = tf.square(y_true - y_pred)
return tf.reduce_mean(squared_difference, axis=-1)
model.compile(optimizer='adam', loss=custom_loss_function)
Keras add_loss() API
As we saw above, the custom loss function in Keras has a restriction to use a specific signature of having y_true and y_pred as arguments. Keras provides another option of add_loss() API which does not have this constraint.
Keras add_loss() API Example
The below cell contains an example of how add_loss() function is used for building loss function.
from keras.layers import Layer
class Custom_layer(Layer):
def __init__(self,rate=1e-2):
super(Custom_layer,self).__init__()
self.rate=rate
def call(self,inputs):
self.add_loss(self.rate*tf.square(inputs))
return inputs
- Also Read – Dummies guide to Cost Functions in Machine Learning [with Animation]
- Also Read – Different Types of Keras Layers Explained for Beginners
- Also Read – Keras Dropout Layer Explained for Beginners
- Also Read – Keras Dense Layer Explained for Beginners
- Also Read – Keras vs Tensorflow vs Pytorch – No More Confusion !!
- Also Read – Keras Convolution Layer – A Beginner’s Guide
- Also Read – Beginners’s Guide to Keras Models API
Conclusion
In this tutorial, we looked at different types of loss functions in Keras, with their syntax and examples. We looked at loss functions for classification and regression problems and lastly, we looked at the custom loss function option of Keras.
Reference Keras Documentation
