Gaussian Naive Bayes Implementation in Python Sklearn

Palash Sharma
Last Updated On May 13, 2021
Python

Table of Contents

Introduction

In this article, we will go through the tutorial for Naive Bayes classification in Python Sklearn. We will understand what is Naive Bayes algorithm and proceed to see an end-to-end example of implementing the Gaussian Naive Bayes classifier in Sklearn with a dataset.

What is Naive Bayes Algorithm?

Naive Bayes is a simple yet powerful probabilistic classification model in machine learning that takes inspiration from Bayes Theorem.

Bayes theorem is a formula that gives a conditional probability of an event A taking place provided another event B has already occurred. Its formula can be written as –

\(P(A|B) = \frac{P(B|A).P(A)}{P(B)}\)

where

A and B are two events
P(A|B) is the probability of event A given event B has already occurred.

P(B|A) is the probability of event B given event A has already occurred.
P(A) is the independent probability of A
P(B) is the independent probability of B

Now, this Bayes theorem can be repurposed to create a classification model as follows –

\(P(y|X) = \frac{P(X|y).P(X)}{P(y)}\)

where

X = x1,x2,x3,.. xN are list of independent predictors

y is the class label
P(y|X) is the probability of label y given the predictors X

The above equation can be expanded as

\(P(y|x1,x2,x3..xN) = \frac{P(x1|y).P(x2|y).P(x3|y)… P(xN|y).P(y)}{P(x1).P(x2).P(x3)…P(xN)}\)

Characteristics of Naive Bayes Classifier

The Naive Bayes algorithm assumes that the predictors have independent and equal contributions in determining the output class.
Naive Bayes model’s assumption that all predictors are independent of each other is not practical in real-world scenarios but still, this assumption gives a good result in most of the cases.
Naive Bayes is commonly used for text classification where data dimensionality is often quite high.

Types of Naive Bayes Classifiers

There are 3 types of Naive Bayes Classifiers –

i) Gaussian Naive Bayes

This classifier is used when the values of predictors are continuous in nature and it is assumed that they follow Gaussian distribution.

ii) Bernoulli Naive Bayes

This classifier is used when the predictors are boolean in nature and it is assumed they follow Bernoulli distribution.

iii) Multinomial Naive Bayes

This classifier uses multinomial distribution and is mostly used for document or text classification problems

Gaussian Naive Bayes Classifier Example in Python Sklearn

In this section, we will take you through an end-to-end example of the Gaussian Naive Bayes classifier in Python Sklearn using a cancer dataset. We will be using the Gaussian Naive Bayes function of SKlearn i.e. GaussianNB() for our example.

1. Loading Initial Libraries

We will start by loading some initial libraries to load and visualize the dataset.

In [1]:

import numpy as np 
import pandas as pd
import matplotlib.pyplot as plt

2. Importing Dataset

Now we will upload the cancer detection dataset that we have obtained from Kaggle for performing our Naive Bayes classification.

In [2]:

dataset = pd.read_csv("datasets/cancer.csv")

3. Exploring Dataset

Let us take an initial look into the dataset with the help of head() function.

In [3]:

dataset.head()

Output:

	id	diagnosis	radius_mean	texture_mean	perimeter_mean	area_mean	smoothness_mean	compactness_mean	concavity_mean	concave points_mean	…	texture_worst	perimeter_worst	area_worst	smoothness_worst	compactness_worst	concavity_worst	concave points_worst	symmetry_worst	fractal_dimension_worst	Unnamed: 32
0	842302	M	17.99	10.38	122.80	1001.0	0.11840	0.27760	0.3001	0.14710	…	17.33	184.60	2019.0	0.1622	0.6656	0.7119	0.2654	0.4601	0.11890	NaN
1	842517	M	20.57	17.77	132.90	1326.0	0.08474	0.07864	0.0869	0.07017	…	23.41	158.80	1956.0	0.1238	0.1866	0.2416	0.1860	0.2750	0.08902	NaN
2	84300903	M	19.69	21.25	130.00	1203.0	0.10960	0.15990	0.1974	0.12790	…	25.53	152.50	1709.0	0.1444	0.4245	0.4504	0.2430	0.3613	0.08758	NaN
3	84348301	M	11.42	20.38	77.58	386.1	0.14250	0.28390	0.2414	0.10520	…	26.50	98.87	567.7	0.2098	0.8663	0.6869	0.2575	0.6638	0.17300	NaN
4	84358402	M	20.29	14.34	135.10	1297.0	0.10030	0.13280	0.1980	0.10430	…	16.67	152.20	1575.0	0.1374	0.2050	0.4000	0.1625	0.2364	0.07678	NaN

5 rows × 33 columns

Next, we will explore the columns present in the dataset through info() function.

In [4]:

dataset.info()

Output:

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 569 entries, 0 to 568
Data columns (total 33 columns):
 #   Column                   Non-Null Count  Dtype  
---  ------                   --------------  -----  
 0   id                       569 non-null    int64  
 1   diagnosis                569 non-null    object 
 2   radius_mean              569 non-null    float64
 3   texture_mean             569 non-null    float64
 4   perimeter_mean           569 non-null    float64
 5   area_mean                569 non-null    float64
 6   smoothness_mean          569 non-null    float64
 7   compactness_mean         569 non-null    float64
 8   concavity_mean           569 non-null    float64
 9   concave points_mean      569 non-null    float64
 10  symmetry_mean            569 non-null    float64
 11  fractal_dimension_mean   569 non-null    float64
 12  radius_se                569 non-null    float64
 13  texture_se               569 non-null    float64
 14  perimeter_se             569 non-null    float64
 15  area_se                  569 non-null    float64
 16  smoothness_se            569 non-null    float64
 17  compactness_se           569 non-null    float64
 18  concavity_se             569 non-null    float64
 19  concave points_se        569 non-null    float64
 20  symmetry_se              569 non-null    float64
 21  fractal_dimension_se     569 non-null    float64
 22  radius_worst             569 non-null    float64
 23  texture_worst            569 non-null    float64
 24  perimeter_worst          569 non-null    float64
 25  area_worst               569 non-null    float64
 26  smoothness_worst         569 non-null    float64
 27  compactness_worst        569 non-null    float64
 28  concavity_worst          569 non-null    float64
 29  concave points_worst     569 non-null    float64
 30  symmetry_worst           569 non-null    float64
 31  fractal_dimension_worst  569 non-null    float64
 32  Unnamed: 32              0 non-null      float64
dtypes: float64(31), int64(1), object(1)
memory usage: 146.8+ KB

From the above information, we can see that id and unnamed:32 columns are not useful, so we can remove them.

In [5]:

dataset = dataset.drop(["id"], axis = 1)

In [6]:

dataset = dataset.drop(["Unnamed: 32"], axis = 1)

3. Visualizing Dataset

To visualize the dataset, we will first split the dataframe into two parts. The first part

contains information about patients who have a malignant (dangerous) tumor and the other half data for benign (safe) tumor.

Malignant Tumor Dataframe

In [8]:

M = dataset[dataset.diagnosis == "M"]

Benign Tumor Dataframe

In [10]:

B = dataset[dataset.diagnosis == "B"]

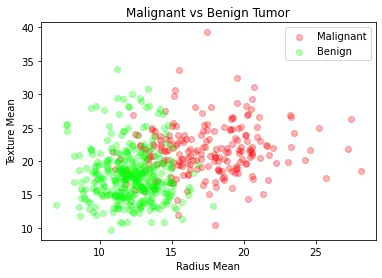
We will now visualize the malignant and benign tumors by looking at the mean radius and mean texture of these tumors.

In [12]:

plt.title("Malignant vs Benign Tumor")
plt.xlabel("Radius Mean")
plt.ylabel("Texture Mean")
plt.scatter(M.radius_mean, M.texture_mean, color = "red", label = "Malignant", alpha = 0.3)
plt.scatter(B.radius_mean, B.texture_mean, color = "lime", label = "Benign", alpha = 0.3)
plt.legend()
plt.show()

Output:

4. Preprocessing

Now we will be assigning a value of ‘1’ to malignant tumors and ‘0’ to benign tumors.

In [13]:

dataset.diagnosis = [1 if i == "M" else 0 for i in dataset.diagnosis]

We now break our dataframe into x and y. The x contains all the independent predictor variables and y contains the prediction of diagnosis.

In [14]:

x = dataset.drop(["diagnosis"], axis = 1)
y = dataset.diagnosis.values

5. Data Normalization

To improve the efficiency of the model it is always good to normalize data to bring them into a common scale.

In [15]:

# Normalization:
x = (x - np.min(x)) / (np.max(x) - np.min(x))

6. Test Train Split

Now with the help of sklearn library train_test_split module, we will split the dataset into training and testing parts.

In [16]:

from sklearn.model_selection import train_test_split

x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.3, random_state = 42)

7. Sklearn Gaussian Naive Bayes Model

Now we will import the Gaussian Naive Bayes module of SKlearn GaussianNB and create an instance of it. We can pass x_train and y_train to fit the model.

In [17]:

from sklearn.naive_bayes import GaussianNB
nb = GaussianNB()
nb.fit(x_train, y_train)

Output:

GaussianNB()

8. Accuracy

The following accuracy score on the test data shows how well our model Sklearn Gaussian Naive Bayes model has performed for predicting cancer.

In [18]:

print("Naive Bayes score: ",nb.score(x_test, y_test))

Output:

Naive Bayes score:  0.935672514619883

Also Read – Linear Regression in Python Sklearn with Example
Also Read – Python Sklearn Logistic Regression Tutorial with Example

Conclusion

Coming to the end of the article, where we explain Naive Bayes and showed you an end-to-end example of implementing Gaussian Naive Bayes in Sklearn with Cancer dataset. Hope this small introductory tutorial was quite helpful for you.

Reference – https://www.kdnuggets.com/2020/06/naive-bayes-algorithm-everything.html

Palash Sharma

I am Palash Sharma, an undergraduate student who loves to explore and garner in-depth knowledge in the fields like Artificial Intelligence and Machine Learning. I am captivated by the wonders these fields have produced with their novel implementations. With this, I have a desire to share my knowledge with others in all my capacity.
View all posts

Tags: python, sklearn

Gaussian Naive Bayes Implementation in Python Sklearn

Introduction

What is Naive Bayes Algorithm?

Characteristics of Naive Bayes Classifier

Types of Naive Bayes Classifiers

i) Gaussian Naive Bayes

ii) Bernoulli Naive Bayes

iii) Multinomial Naive Bayes

Gaussian Naive Bayes Classifier Example in Python Sklearn

1. Loading Initial Libraries

2. Importing Dataset

3. Exploring Dataset

3. Visualizing Dataset

4. Preprocessing

5. Data Normalization

6. Test Train Split

7. Sklearn Gaussian Naive Bayes Model

8. Accuracy

Conclusion

Leave a Reply Cancel reply

Latest Posts

Follow US