Introduction
In this article, we will go through the tutorial for implementing logistic regression using the Sklearn (a.k.a Scikit Learn) library of Python. We will have a brief overview of what is logistic regression to help you recap the concept and then implement an end-to-end project with a dataset to show an example of Sklean logistic regression with LogisticRegression() function.
What is Logistic Regression?
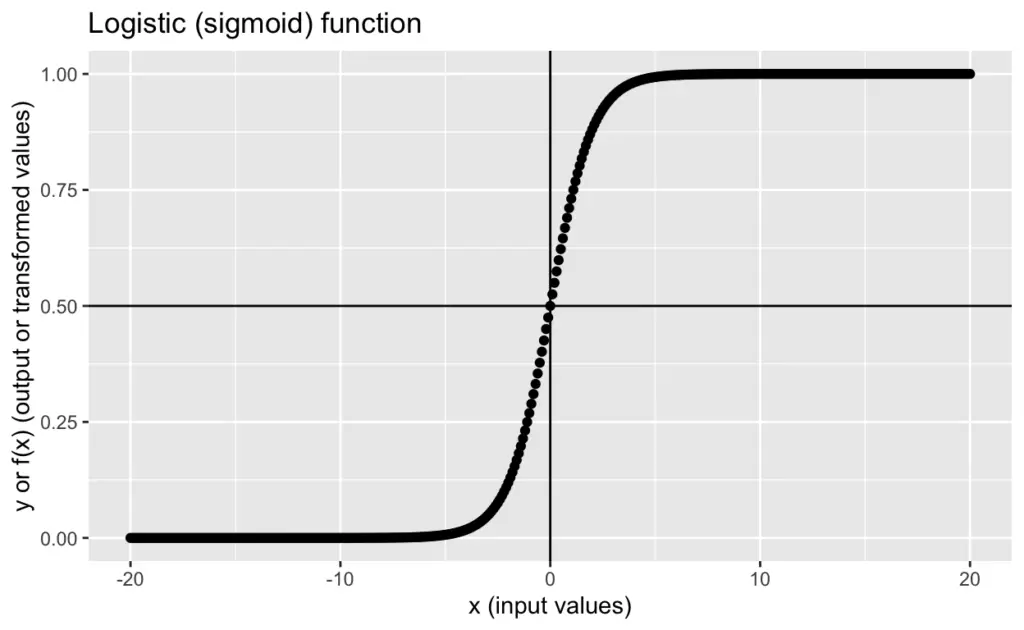
Contrary to its name, logistic regression is actually a classification technique that gives the probabilistic output of dependent categorical value based on certain independent variables.
Logistic regression uses the logistic function to calculate the probability.
- Also Read – Linear Regression in Python Sklearn with Example
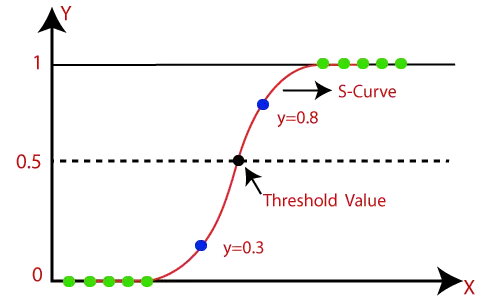
Usually, for doing binary classification with logistic regression, we decide on a threshold value of probability above which the output is considered as 1 and below the threshold, the output is considered as 0.
In the below illustration, the probability outcome y=0.8 will be treated as a positive class (i.e. 1) and y=0.3 as the negative class (i.e. 0)
Example of Logistic Regression in Python Sklearn
For performing logistic regression in Python, we have a function LogisticRegression() available in the Scikit Learn package that can be used quite easily.
Let us understand its implementation with an end-to-end project example below where we will use credit card data to predict fraud.
i) Loading Libraries
The very first step is to load the libraries that will be required for building the model.
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import Pipeline
from sklearn.metrics import roc_curve, roc_auc_score, classification_report, accuracy_score, confusion_matrix
import seaborn as sns
import matplotlib.pyplot as plt
ii) Load data
Now we will be loading the dataset into our environment. This dataset is obtained from Kaggle. It contains information about credit card transactions. They are classified as fraudulent and non-fraudulent transactions.
credit_card = pd.read_csv('datasets/creditcard.csv')
iii) Visualize Data
f, ax = plt.subplots(figsize=(7, 5))
sns.countplot(x='Class', data=credit_card)
_ = plt.title('# Fraud vs NonFraud')
_ = plt.xlabel('Class (1==Fraud)')
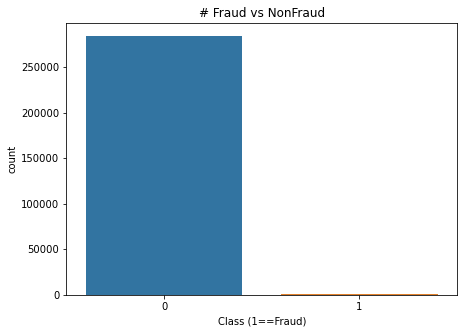
The bar plot shows that in the dataset we have the majority of non-fraudulent transactions. This type of problem will give rise to the imbalanced class problem.
If we build a model with the help of this dataset then the classifier would always predict transactions as non-fraudulent. This will result in a classifier with high accuracy but it will be of no use.
The following code snippet output shows the accuracy expected of this model
base_line_accuracy = 1-np.sum(credit_card.Class)/credit_card.shape[0]
base_line_accuracy
0.9982725143693799
Since the accuracy won’t be useful for model evaluation, so we will use the AUC ROC score for checking the model quality.
iv) Splitting into Training and Test set
First, we will segregate the independent variables in data frames X and the dependent variable in data frame y.
Next, we split the dataset into training and testing sets with the help of train_test_split() function.
X = credit_card.drop(columns='Class', axis=1)
y = credit_card.Class.values
np.random.seed(42)
X_train, X_test, y_train, y_test = train_test_split(X, y)
v) Model Building and Training
Before we build the model, we use the standard scaler function to scale the values into a common range. Next, we create an instance of LogisticRegression() function for logistic regression.
We are not passing any parameters to LogisticRegression() so it will assume default parameters. Some of the important parameters you should know are –
- penalty: Default = L2 – It specifies the norm for the penalty
- C: Default = 1.0 – It is the inverse of regularization strength
- solver: Default = ‘lbfgs’ – It denotes the optimizer algorithm
Here we are also making use of Pipeline to create the model to streamline standard scalar and model building.
In [7]:
scaler = StandardScaler()
lr = LogisticRegression()
model1 = Pipeline([('standardize', scaler),
('log_reg', lr)])
In the next step, we fit our model to the training data with the help of fit() function.
model1.fit(X_train, y_train)
Pipeline(steps=[('standardize', StandardScaler()),
('log_reg', LogisticRegression())])
vi) Training Score
Now to evaluate the model on the training set we create a confusion matrix that will help in knowing the true positives, false positives, false negatives, and true negatives. Also, the roc_auc_score() function will help in fetching the area under the receiver-operator-curve for the model that we have built.
We also calculate accuracy score, even though we discussed that accuracy score can be misleading for an imbalanced dataset.
y_train_hat = model1.predict(X_train)
y_train_hat_probs = model1.predict_proba(X_train)[:,1]
train_accuracy = accuracy_score(y_train, y_train_hat)*100
train_auc_roc = roc_auc_score(y_train, y_train_hat_probs)*100
print('Confusion matrix:\n', confusion_matrix(y_train, y_train_hat))
print('Training AUC: %.4f %%' % train_auc_roc)
print('Training accuracy: %.4f %%' % train_accuracy)
Confusion matrix: [[213198 28] [ 135 244]] Training AUC: 98.0170 % Training accuracy: 99.9237 %
vii) Testing Score
We will now calculate the confusion matrix, AUC ROC, and accuracy of the model with the testing data set.
The result shows that our built model is able to detect 68 fraudulent transactions from 113 transactions. There is a recall of 60% and also there are only 12 false positives, this is very less as compared to the size of data.
y_test_hat = model1.predict(X_test)
y_test_hat_probs = model1.predict_proba(X_test)[:,1]
test_accuracy = accuracy_score(y_test, y_test_hat)*100
test_auc_roc = roc_auc_score(y_test, y_test_hat_probs)*100
print('Confusion matrix:\n', confusion_matrix(y_test, y_test_hat))
print('Testing AUC: %.4f %%' % test_auc_roc)
print('Testing accuracy: %.4f %%' % test_accuracy)
Confusion matrix: [[71077 12] [ 45 68]] Training AUC: 97.4516 % Training accuracy: 99.9199 %
To get more clarity let us use classification_report() function for getting the precision and recall of the model for the test dataset.
If we look at the f1-score for row 1, we come to know that our model is able to identify 70% fraud cases.
print(classification_report(y_test, y_test_hat, digits=6))
precision recall f1-score support
0 0.999367 0.999831 0.999599 71089
1 0.850000 0.601770 0.704663 113
accuracy 0.999199 71202
macro avg 0.924684 0.800801 0.852131 71202
weighted avg 0.999130 0.999199 0.999131 71202
We can further try to improve this model performance by hyperparameter tuning by changing the value of C or choosing other solvers available in LogisticRegression().
We can also try to improve performance by balancing the dataset by using SMOTE algorithm available in scikit learn imblearn module. These are advanced topics that we will cover later in another tutorial.
- Also Read – Linear Regression in Python Sklearn with Example
Conclusion
Hope you liked our tutorial and now understand how to implement logistic regression with Sklearn (Scikit Learn) in Python. We showed you an end-to-end example using a dataset to build a logistic regression model for the predictive task using SKlearn LogisticRegression() function. The tutorial also shows that we should not rely on accuracy scores to determine the performance of imbalanced datasets.
-
I am Palash Sharma, an undergraduate student who loves to explore and garner in-depth knowledge in the fields like Artificial Intelligence and Machine Learning. I am captivated by the wonders these fields have produced with their novel implementations. With this, I have a desire to share my knowledge with others in all my capacity.
View all posts


