Neural Network Primitives Part 1 – McCulloch Pitts Neuron Model (1943)

Introduction

Modern machine learning world is going crazy over deep learning. People are stacking hundreds and thousands of interconnected artificial neurons to build the most complex of deep neural network than ever. These deep neural nets are able to create the most astonishing AIs that are outperforming humans in many tasks. But just like complex living forms, which evolved from the primitive cellular life, even the deep neural network had its humble beginning as a primitive artificial neuron dating back to McCulloch-Pitts Neuron Model in 1943.

• Also Read – Machine Learning Examples – A motivation for beginners

Neural Network Primitives is a series to understand the primitive forms of the artificial neural networks and how these were the first building blocks of modern deep learning. In this first part we will understand the first ever artificial neuron known as McCulloch-Pitts Neuron Model.

• Also Read – Neural Network Primitives Part 2 – Perceptron Model (1957)
• Also Read – Neural Network Primitives Part 3 – Sigmoid Neuron
• Also Read- Neural Network Primitives Final Part 4 – Modern Artificial Neuron

McCulloch-Pitts Neuron Model

Artificial Neural Network essentially tries to mimic a real biological neural network and so without surprise the first ever primitive model was conceptualized by Warren Sturgis McCulloch  and Walter Harry Pitts in 1943 who came from Neuropsychology and Computational Neuroscience backgrounds.

Different parts of McCulloch-Pitts Neuron Model

McCulloch-Pitts neuron model’s anatomy is very simple and has following parts –

1. Neuron
2. Excitatory Input
3. Inhibitory Input
4. Output

Neuron

Neuron is a computational unit which has incoming input signals. The input signals are computed and an output is fired. The neuron further consists of following two elements –

Summation Function

This simply calculates the sum of incoming inputs(excitatory).

Activation Function

Essentially activation function in this case is the step function which sees if the summation is more than equal to a preset Threshold value , if yes then neuron should fire (i.e. output =1 ) if not the neuron should not fire (i.e. output =0).

• Neuron fires: Output =1 , if Summation >= Threshold
• Neuron does not fires: Output =0 , if Summation < Threshold

Excitatory Input

This is an incoming binary signals to neuron, which can have only two values 0 or 1. the value of 0 indicates that the input is off, whereas the value of 1 indicates that the input is on.

Inhibitory Input

This is another type of input signal to neuron. If this input is on, this will now allow neuron to fire , even if there are other excitatory inputs which are on.

Output

This is simply the output of the neuron which again can take only binary values of 0 or 1. The value of 0 indicates that the neuron does not fire, the value of 1 indicates the neuron does fire.

[adrotate banner=”3″]

How McCulloch-Pitts Neuron Model works

Having explained the entire set up of McCulloch-Pitts neuron model in the above section, let us now understand how this model works.

1. The input signals are switched on and the neuron is activated.
2. If Neuron detects that Inhibitory input is switched on, the output is straightaway zero, which means the neuron does not fire.
3. If there is no Inhibitory input, then neuron proceeds to calculate the sum of number of excitatory inputs that are switched on.
4. If this sum is greater than equal to the preset threshold value, the neuron fires (output=1) , otherwise the neuron does not fire (output=0)

The above steps are shown in the animation below for better visualization.

Designing McCulloch-Pitts neuron model

McCulloch-Pitts neuron model can be used to compute some simple functions which involves binary input and output.  Let us design 2 input McCulloch-Pitts neuron model for  two well known logical functions –  AND function and OR function.  And then we will design a model for a real life relate able example.

We will see that for designing a McCulloch-Pitts neuron model it all comes down to choosing a right Threshold value for the given problem in hand.

AND Function

In AND function, for the neuron to fire all the 2 excitatory nput signals have to be enabled. So it is very intuitive that the threshold value should be 2 here. Additionally if the inhibitory input is on, then irrespective of any other input, the neuron will not fire.

We can summarize the behavior of neuron for AND function in the below table. You can see that when Inhibitory input is on, the neuron would not fire even if the other two excitatory inputs satisfy the threshold condition.

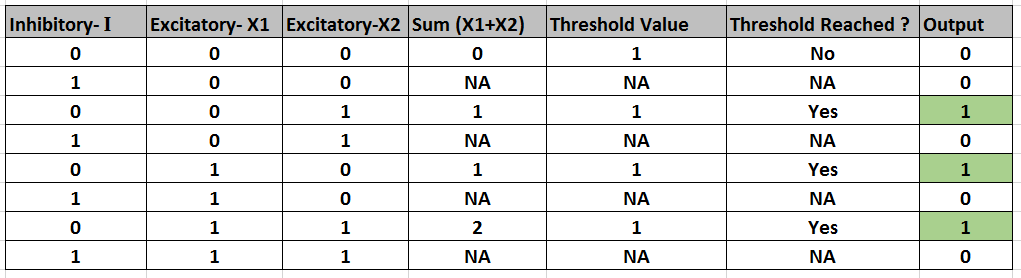
OR Function

In OR function, for the neuron to fire at least one excitatory input signals has to be enabled. So it is very intuitive that the threshold value should be 1 here. Again if the inhibitory input is on, then irrespective of any other input, the neuron will not fire.

We can summarize the behavior of neuron for OR function in the below table. You can see that when Inhibitory input is on, the neuron would not fire even if the other two excitatory inputs satisfy the threshold condition.

A silly real life example

To give you a more better feel of what is going on over here let us create a hypothetical situation where our McCulloch-Pitts neuron model will take a decision for us.

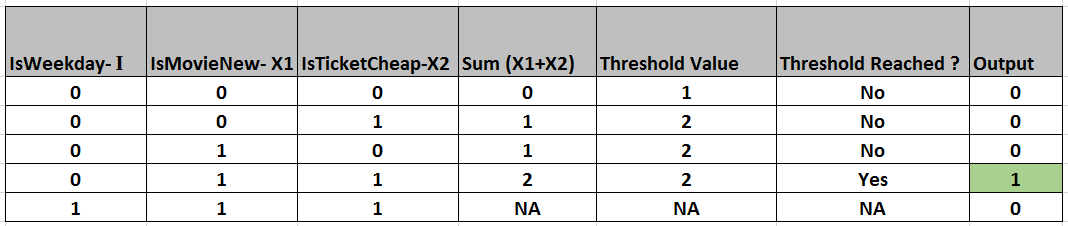
So you like going to for a particular movie if is is a new release. But you are also cautious about price of movie tickets. You watch a movie if the ticket price is cheap.

Further you cant plan movie on your weekdays as they are busy as hell.

Neuron design

Our neuron will consist of two excitatory inputs –

1. X1- IsMovieNew
2. X2- IsTicketCheap

Now as per given problem, you will go to particular movie only if when both IsMovieNew and  IsTicketCheap inputs of the neuron are on.

As you can guess, this is essentially a AND function problem and the Threshold value will be 2.

But wait a minute, if its weekday you cant even think of planning for a movie outing. So we will also have a Inhibitory input –

I – IsWeekday

When IsWeekday is on for the neuron, then there is no question of planning for the movie.

And finally we have output of the neuron. Output =1 means you should plan to go for a particular movie, Output = 0 means you should not plan.

So this is the complete design of the neuron that will decide if you should go for a particular movie or not.

We can summarize the behavior of the neuron in below table.

Some points to consider

• McCulloch-Pitts neuron model can only deal with binary inputs and binary output.
• Since it deals with only binary values McCulloch-Pitts neuron can’t work with real life values like years, price, age etc.
• This model considers that all inputs are equal. But in real life world it might not be the case. In our above example, for you – the price of the movie might play little role in deciding the plan and new movie play more value for making plan. But we can’t assign such weights to inputs of McCulloch-Pitts neuron.
• Using this approach we can create neuron models for only those problems that are linearly separable.
• As you could intuitively see McCulloch-Pitts neuron can be used to represents logical functions. But then it cannot represen XOR logical function it is not linearly separable.
• And finally we are just calculating the threshold value ourself, which is the only parameter of the model. And this leads to our final topic of discussion below.

No (Machine) Learning in McCulloch-Pitts Neuron Model

Well, may be you had guessed it by now that there is no learning involved in McCulloch-Pitts neuron model. Based on the scenario and set of possible inputs involved we are calculating the threshold value and building the model. There is no learning taking place which is not how a machine learning model should look like, right?

Well, this model was not built to work as machine learning model in the first place. Rather McCulloch and Pitts just wanted to build a mathematical model to represent the workings of biological neuron. But this humble looking model actually inspired other researchers to come up with true machine learning based neural models in the later years.

• Also Read – Neural Network Primitives Part 2 – Perceptron Model (1957)
• Also Read – Neural Network Primitives Part 3 – Sigmoid Neuron
• Also Read- Neural Network Primitives Final Part 4 – Modern Artificial Neuron

In The End…

I hope this was a good and simple read to understand the origins of modern Deep learning and Neural Networks.

McCulloch-Pitts neuron model is of historic importance for being the inspiration of what became Neural Network later years. And this has now become a complex world of Deep Learning. If you actually look at modern neural networks, they are just the sophisticated version of this primitive McCulloch-Pitts neuron model. At the core of it they all are similar in essence.

Do share your feed back about this post in the comments section below. If you found this post informative, then please do share this and subscribe to us by clicking on bell icon for quick notifications of new upcoming posts. And yes, don’t forget to join our new community MLK Hub and Make AI Simple together.