Cross Validation in Sklearn | Hold Out Approach | K-Fold Cross Validation | LOOCV

Veer Kumar
Last Updated On February 6, 2022
Python

Introduction:

In today’s tutorial, we will see various techniques of cross-validation in Sklearn such as K-fold cross-validation, Stratified K-fold cross-validation, Leave one out cross-validation(LOOCV), and Repeated random train test splits. We will look into how these cross-validation techniques help better evaluation of machine learning models along with examples.

K-Fold Cross Validation in Sklearn — Source

What is Cross-Validation in Machine Learning

When we create a machine learning model with supervised learning techniques it is very important to evaluate the performance and robustness of the model before moving it to production.

Key aspects of evaluating the quality of the model are –

How accurate the model is
How generalized the model is

When we start building a model and train it with the ‘entire’ dataset, we can very well calculate its accuracy on this training data set. But we cannot test how this model will behave with new data which is not present in the training set, hence its generalization cannot be determined.

Hence we need techniques to make use of the same data set for both training and testing of the models.

In machine learning, Cross-Validation is the technique to evaluate how well the model has generalized and its overall accuracy. For this purpose, it randomly samples data from the dataset to create training and testing sets. There are multiple cross-validation approaches as follows –

Hold Out Approach

Leave One Out Cross-Validation
K-Fold Cross-Validation
Stratified K-Fold Cross-Validation

Repeated Random Train Test Split

1. Hold Out Approach

In the hold-out approach, the data set is split into the train and test set with random sampling. The train set is used for training the model and the test set is used to test its accuracy with unseen data. If the training and accuracy are almost the same then the model is said to have generalized well. It is common to use 80% of data for training and the remaining 20% for testing.

Advantages

It is simple and easy to implement

The execution time is less.

Disadvantages

If the dataset itself is small, setting aside portions for testing would reduce the robustness of the model. This is because the training sample may not be representative of the entire dataset.
The evaluation metrics may vary due to the randomness of the split between the train and test set.

Although 80-20 split for train test is widely followed, there is no thumb rule for the split and hence the results can vary based on how the train test split is done.

2. Leave One Out Cross Validation (LOOCV)

In this technique, if there are n observations in the dataset, only one observation is reserved for testing, and the remaining data points are used for training. This is repeated n times till all data points have been used for testing purposes in each iteration. Finally, the average accuracy is calculated by combining the accuracies of each iteration.

Advantage

Since every data participates both for training and testing, the overall accuracy is more reliable.

It is very useful when the dataset is small.

Disadvantage

LOOCV is not practical to use when the number of data observations n is huge. E.g. imagine a dataset with 500,000 records, then 500,000 model needs to be created which is not really feasible.
There is a huge computational and time cost associated with the LOOCV approach.

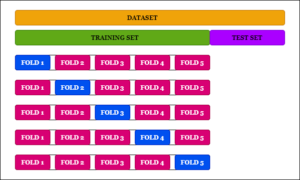
3. K-Fold Cross-Validation

In the K-Fold Cross-Validation approach, the dataset is split into K folds. Now in 1st iteration, the first fold is reserved for testing and the model is trained on the data of the remaining k-1 folds.

In the next iteration, the second fold is reserved for testing and the remaining folds are used for training. This is continued till the K-th iteration. The accuracy obtained in each iteration is used to derive the overall average accuracy for the model.

Advantages

K-Fold cross-validation is useful when the dataset is small and splitting it is not possible to split it in train-test set (hold out approach) without losing useful data for training.

It helps to create a robust model with low variance and low bias as it is trained on all data

Disadvantages

The major disadvantage of K-Fold Cross Validation is that the training needs to be done K times and hence it consumes more time and resources,
Not recommended to be used with sequential time series data.

When the dataset is imbalanced, K-fold cross-validation may not give good results. This is because some folds may have just a few or no records for the minority class.

4. Stratified K-Fold Cross-Validation

Stratified K-fold cross-validation is useful when the data is imbalanced. While sampling data into K-folds it makes sure that the distribution of all classes in each fold is maintained. For example, if in the dataset 98% of data belongs to class B and 2% to class A, the stratified sampling will make sure each fold contains the two classes in the same ratio of 98% to 2%.

Advantage

Stratified K-fold cross-validation is recommended when the dataset is imbalanced.

5. Repeated Random Test-Train Split

Repeated random test-train split is a hybrid of traditional train-test splitting and the k-fold cross-validation method. In this technique, we create random splits of the data into the training-test set and then repeat this process multiple times, just like the cross-validation method.

Examples of Cross-Validation in Sklearn Library

About Dataset

We will be using Parkinson’s disease dataset for all examples of cross-validation in the Sklearn library. The goal is to predict whether or not a particular patient has Parkinson’s disease. We will be using the decision tree algorithm in all the examples.

The dataset has 21 attributes and 195 rows. The various fields of the Parkinson’s Disease dataset are as follows –

MDVP:Fo(Hz) – Average vocal fundamental frequency
MDVP:Fhi(Hz) – Maximum vocal fundamental frequency
MDVP:Flo(Hz) – Minimum vocal fundamental frequency

MDVP:Jitter(%),MDVP:Jitter(Abs),MDVP:RAP,MDVP:PPQ,Jitter:DDP – Several
measures of variation in fundamental frequency
MDVP:Shimmer,MDVP:Shimmer(dB),Shimmer:APQ3,Shimmer:APQ5,MDVP:APQ,Shimmer:DDA – Several measures of variation in amplitude

NHR,HNR – Two measures of ratio of noise to tonal components in the voice
status – Health status of the subject (one) – Parkinson’s, (zero) – healthy
RPDE,D2 – Two nonlinear dynamical complexity measures

DFA – Signal fractal scaling exponent
spread1,spread2PPE – Three nonlinear measures of fundamental frequency variation

Also Read – Decision Tree Classifier in Python Sklearn with Example

Importing Necessary Libraries

We first load the libraries required to build our model.

In [53]:

import pandas as pd
import numpy as np
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn.model_selection import KFold
from sklearn.model_selection import StratifiedKFold

Reading CSV Data into Pandas

Next, we load the dataset in the CSV file into the pandas dataframes and check the top 5 rows.

In [52]:

df=pd.read_csv(r"C:\Users\Veer Kumar\Downloads\Parkinsson disease.csv")
df.head()

Out[52]:

	name	MDVP:Fo(Hz)	MDVP:Fhi(Hz)	MDVP:Flo(Hz)	MDVP:Jitter(%)	MDVP:Jitter(Abs)	MDVP:RAP	MDVP:PPQ	Jitter:DDP	MDVP:Shimmer	…	Shimmer:DDA	NHR	HNR	status	RPDE	DFA	spread1	spread2	D2	PPE
0	phon_R01_S01_1	119.992	157.302	74.997	0.00784	0.00007	0.00370	0.00554	0.01109	0.04374	…	0.06545	0.02211	21.033	1	0.414783	0.815285	-4.813031	0.266482	2.301442	0.284654
1	phon_R01_S01_2	122.400	148.650	113.819	0.00968	0.00008	0.00465	0.00696	0.01394	0.06134	…	0.09403	0.01929	19.085	1	0.458359	0.819521	-4.075192	0.335590	2.486855	0.368674
2	phon_R01_S01_3	116.682	131.111	111.555	0.01050	0.00009	0.00544	0.00781	0.01633	0.05233	…	0.08270	0.01309	20.651	1	0.429895	0.825288	-4.443179	0.311173	2.342259	0.332634
3	phon_R01_S01_4	116.676	137.871	111.366	0.00997	0.00009	0.00502	0.00698	0.01505	0.05492	…	0.08771	0.01353	20.644	1	0.434969	0.819235	-4.117501	0.334147	2.405554	0.368975
4	phon_R01_S01_5	116.014	141.781	110.655	0.01284	0.00011	0.00655	0.00908	0.01966	0.06425	…	0.10470	0.01767	19.649	1	0.417356	0.823484	-3.747787	0.234513	2.332180	0.410335

5 rows × 24 columns

Data Preprocessing

The “name” column is not going to add any value in training the model and can be discarded, so we are dropping it below.

In [33]:

df.drop(df.columns[0], axis = 1, inplace = True)

Next, we will separate the feature and target matrix as shown below.

In [35]:

#Independent And dependent features
X=df.drop('status', axis=1)
y=df['status']

Hold out Approach in Sklearn

The hold-out approach can be applied by using train_test_split module of sklearn.model_selection

In the below example we have split the dataset to create the test data with a size of 30% and train data with a size of 70%. The random_state number ensures the split is deterministic in every run.

In [38]:

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.30, random_state=4)

model = DecisionTreeClassifier()
model.fit(X_train, y_train)

result = model.score(X_test, y_test)
print(result)

Out[38]:

0.7796610169491526

K-Fold Cross-Validation

K-Fold Cross-Validation in Sklearn can be applied by using cross_val_score module of sklearn.model_selection.

In the below example, 10 folds are used that produced 10 accuracy scores using which we calculated the mean score.

In [40]:

from sklearn.model_selection import cross_val_score

model=DecisionTreeClassifier() 
kfold_validation=KFold(10)

results=cross_val_score(model,X,y,cv=kfold_validation)
print(results)
print(np.mean(results))

Out[40]:

[0.7        0.8        0.8        0.8        0.8        0.78947368
 0.84210526 1.         0.68421053 0.36842105]
0.758421052631579

Stratified K-fold Cross-Validation

In Sklearn stratified K-fold cross-validation can be applied by using StratifiedKFold module of sklearn.model_selection

In the below example, the dataset is divided into 5 splits or folds. It returns 5 accuracy scores using which we calculate the final mean score.

In [41]:

from sklearn.model_selection import StratifiedKFold

skfold=StratifiedKFold(n_splits=5)

model=DecisionTreeClassifier()
scores=cross_val_score(model,X,y,cv=skfold)

print(scores)
print(np.mean(scores))

Out[41]:

array([0.61538462, 0.79487179, 0.71794872, 0.74358974, 0.71794872])

0.717948717948718

Leave One Out Cross Validation(LOOCV)

In Sklearn Leave One Out Cross Validation (LOOCV) can be applied by using LeaveOneOut module of sklearn.model_selection

In [43]:

from sklearn.model_selection import LeaveOneOut

model=DecisionTreeClassifier()

leave_validation=LeaveOneOut()

results=cross_val_score(model,X,y,cv=leave_validation)

results

Out[22]:

array([1., 1., 1., 1., 1., 0., 1., 1., 1., 1., 1., 1., 1., 0., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 0., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 0., 0., 1., 1., 1., 0., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       0., 1., 1., 1., 1., 0., 1., 1., 1., 1., 1., 1., 1., 0., 1., 1., 1.,
       1., 0., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 0., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 0., 1., 1., 1., 1., 1., 1., 1., 1., 0.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 0., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 0.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 0., 1., 1., 1., 1., 1., 1.,
       1., 0., 1., 1., 1., 1., 1., 1., 1., 1., 1., 0., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 0., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 0., 1., 1., 1., 1., 1., 1., 1.,
       0., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 0., 1., 1., 1., 1., 1., 0., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       0., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 0., 1., 1., 0., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 0., 0., 1., 1., 0., 1., 1., 1., 1., 1., 0., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 0., 1., 1., 1., 1., 1., 1., 1., 1., 1., 0., 1.,
       1., 1., 0., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 0., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 0., 1., 0., 0., 1., 1., 1.,
       1., 0., 1., 1., 1., 1., 1., 1., 0., 1., 1., 1., 1., 1., 1., 0., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 0., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 0., 0.,
       1., 1., 1., 1., 1., 1., 1., 1.])

In [44]:

print(np.mean(results))

Out[44]:

0.8358974358974359

Repeated Random Test-Train Splits

In Sklearn repeated random test-train splits can be applied by using ShuffleSplit module of sklearn.model_selection

In [45]:

from sklearn.model_selection import ShuffleSplit

model=DecisionTreeClassifier()
ssplit=ShuffleSplit(n_splits=10,test_size=0.30)
results=cross_val_score(model,X,y,cv=ssplit)

print(results)
print(np.mean(results))

Out[45]:

array([0.79661017, 0.71186441, 0.79661017, 0.88135593, 0.72881356,
       0.84745763, 0.83050847, 0.77966102, 0.83050847, 0.81355932])

0.8016949152542372

Veer Kumar

I am passionate about Analytics and I am looking for opportunities to hone my current skills to gain prominence in the field of Data Science.
View all posts

Tags: machine learning, python, scikit learn, sklearn

Cross Validation in Sklearn | Hold Out Approach | K-Fold Cross Validation | LOOCV

Introduction:

What is Cross-Validation in Machine Learning

1. Hold Out Approach

Advantages

Disadvantages

2. Leave One Out Cross Validation (LOOCV)

Advantage

Disadvantage

3. K-Fold Cross-Validation

Advantages

Disadvantages

4. Stratified K-Fold Cross-Validation

Advantage

5. Repeated Random Test-Train Split

Examples of Cross-Validation in Sklearn Library

About Dataset

Importing Necessary Libraries

Reading CSV Data into Pandas

Data Preprocessing

Hold out Approach in Sklearn

K-Fold Cross-Validation

Stratified K-fold Cross-Validation

Leave One Out Cross Validation(LOOCV)

Repeated Random Test-Train Splits

Leave a Reply Cancel reply

Latest Posts

Follow US