Introduction
In this article, we are going to see the tutorial for Bilateral Filtering in OpenCV python for image smoothing. We will see its syntax of the function cv2.bilateralFilter() and its example for a better understanding of beginners. Before we are going to start this tutorial let’s understand the motivation to read another Image smoothing method irrespective of the fact that we have already studied three types of filtering techniques i.e Averaging Blur, Gaussian Blur, and Median Blur.
What is Bilateral Filtering?
According to Wikipedia –
“A bilateral filter is a non-linear, edge-preserving, and noise-reducing smoothing filter for images. It replaces the intensity of each pixel with a weighted average of intensity values from nearby pixels.”
Let us see some mathematics behind this Bilateral filtering method, but before that, it will be good to quickly cover Gaussian filtering since the Gaussian filter is very close to the Bilateral filter.
Gaussian Filtering (Initial Concept for Bilateral Filtering)
Mathematically, Gaussian Blur(GB) filtered image is given by:
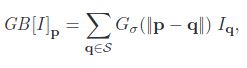
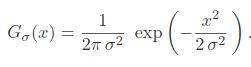
Basically (Gσ) is a spatial Gaussian that decreases the influence of distant pixels.
Bilateral Filtering (In-depth)
Let’s understand Bilateral filtering in more detail now.
As we have seen above, in Gaussian filter only nearby pixels are considered while filtering. It doesn’t consider whether pixels have almost the same intensity. It doesn’t consider whether a pixel is an edge pixel or not. So it blurs the edges also, which we don’t want to do since it takes away crucial details from the image.
Bilateral filtering also takes a Gaussian filter in space, but additionally considers one more Gaussian filter which is a function of pixel difference. The Gaussian function of space makes sure that only nearby pixels are considered for blurring, while the Gaussian function of intensity difference makes sure that only those pixels with similar intensities to the central pixel are considered for blurring. So it preserves the edges since pixels at edges will have large intensity variation.
The important point which is considered in Bilateral filtering is that the two pixels are close to each other not only if they occupy nearby spatial locations but also if they have some similarity in the photometric range. These properties of bilateral filtering overcome the drawback of other techniques like Averaging Blur, Gaussian Blur, and Median Blur since it is able to preserve edges.
Bilateral Filtering – Maths
Mathematically Bilateral filter is given by the following equation BF
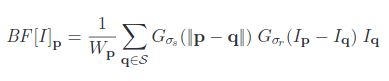
where Wp is a normalization factor
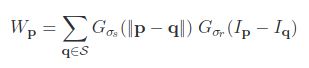
So as we see here two new terms are added in Gaussian filter to become the bilateral filter
The first one is this term –
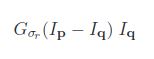
And the second one is this –
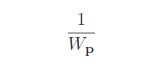
- Now we already know from Gaussian filtering that Gσs is a spatial Gaussian that decreases the influence of distant pixels.
- The second term is added Gσr which is a range Gaussian that decreases the influence of pixels q with an intensity value different from Ip.
- σs are the space parameter and σr are the range parameter.
- σs represents the spatial extent of the kernel size of the considered neighborhood and σr represents the minimum amplitude of an edge. This means that parameters σs and σr will measure the amount of filtering for the image “I”.
Note: range means quantities related to pixel values i.e intensities while space refers to the pixel location.
The main idea behind this mathematics of Bilateral Filtering is that
- Each pixel is replaced by a weighted average of its neighbors.
- Each neighbor is weighted by a spatial component that penalizes distant pixels and range component that penalizes pixels with a different intensity.
- The combination of both components ensures that only nearby similar pixels contribute to the final result.
The bilateral filter is controlled by two parameters: σs and σr
- If range parameter σr increases, the bilateral filter becomes closer to Gaussian blur
- Increasing the spatial parameter σs smooths larger features
Bilateral Filtering in Python OpenCV – cv2.bilateralFilter()
For performing Bilateral Filtering in Python OpenCV, there is a function called bilateralFilter(). Below is its syntax –
Syntax
cv2.bilateralFilter ( src, dst, d, sigmaColor,sigmaSpace, borderType = BORDER_DEFAULT )
Parameters
- src It is the image whose is to be blurred
- dst Destination image of the same size and type as src .
- d Diameter of each pixel neighborhood that is used during filtering. If it is non-positive, it is computed from sigmaSpace.
- sigmaColor Filter sigma in the color space. A larger value of the parameter means that farther colors within the pixel neighborhood will be mixed together, resulting in larger areas of semi-equal color.
- sigmaSpace Filter sigma in the coordinate space. A larger value of the parameter means that farther pixels will influence each other as long as their colors are close enough. When d>0, it specifies the neighborhood size regardless of sigmaSpace. Otherwise, d is proportional to sigmaSpace.
- borderType border mode used to extrapolate pixels outside of the image
Example of Bilateral Filtering in Python OpenCV
In this section, we will apply Bilateral filtering in Python OpenCV using bilateralFilter() on an example image. But to appreciate how bilateral filtering preserves the edges during image smoothing we will also apply Gaussian filtering on the same image.
But first, let us import the required library and import the sample image for our example.
Importing OpenCV library and Sample Image
import cv2
#read image
img=cv2.imread("bilateral.jpg")
#Display image
window_name='imagefirst'
cv2.namedWindow(window_name, cv2.WINDOW_NORMAL)
cv2.imshow(window_name,img)
cv2.waitKey(0)
cv2.destroyAllWindows()
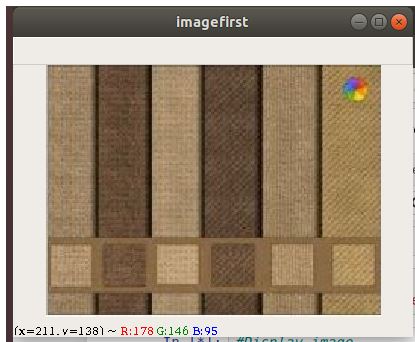
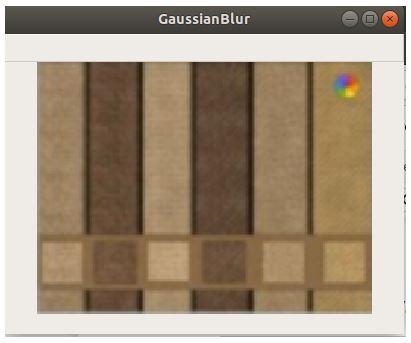
Blurring using cv2.GaussianBlur()
gaussian_blur = cv2.GaussianBlur(img,(5,5),sigmaX=0)
#Display image
window_name='GaussianBlur'
cv2.namedWindow(window_name, cv2.WINDOW_NORMAL)
cv2.imshow(window_name,gaussian_blur)
cv2.waitKey(0)
cv2.destroyAllWindows()
Example: Bilateral Filtering with cv2.bilateralFilter()
bilateral_blur = cv2.bilateralFilter(img,15,80,80)
#Display image
window_name='bilateralfilterimage'
cv2.namedWindow(window_name, cv2.WINDOW_NORMAL)
cv2.imshow(window_name,bilateral_blur)
cv2.waitKey(0)
cv2.destroyAllWindows()
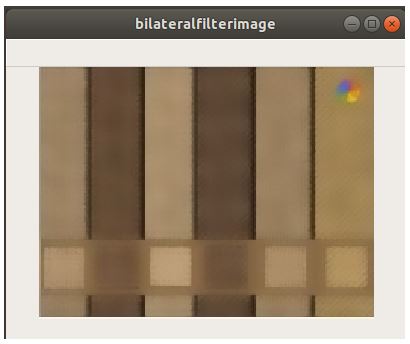
As we can see here that the image smoothing or blurring effect achieved by bilateral filtering has preserved the edges beautifully and distinctively when compared to gaussian blurring.
Conclusion
Reaching the end of this tutorial, we learned how we can do smoothing on an image using Bilateral Filtering. We covered the fundamental concepts in detail and also saw an example of bilateral filtering with Python OpenCV function cv2.bilateralFilter(). We also did the comparison of cv2.bilateralFilter() output with that of other techniques of gaussian blur using cv2.GaussianBlur().
