Introduction
In this tutorial, we are learning about different PyTorch loss functions that you can use for training neural networks. These loss functions help in computing the difference between the actual output and expected output which is an essential way of how neural network learns. Here we will guide you to pick appropriate PyTorch loss functions for regression and classification for your requirement.
But before that let us understand what is loss function in the first place and why they are needed.
What is Loss Function?
Loss Functions, also known as cost functions, are used for computing the error between expected output and actual output during the training phase. The goal of the training phase is to reduce the error as much as possible, in other words, optimize the loss function.
The below illustration should able to give you the intuition of cost or loss functions.
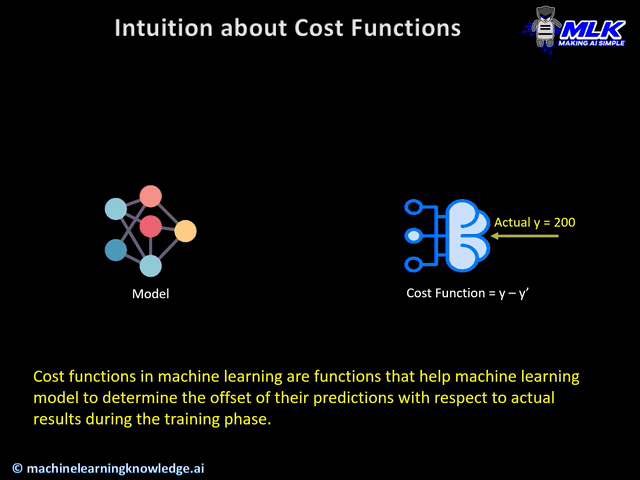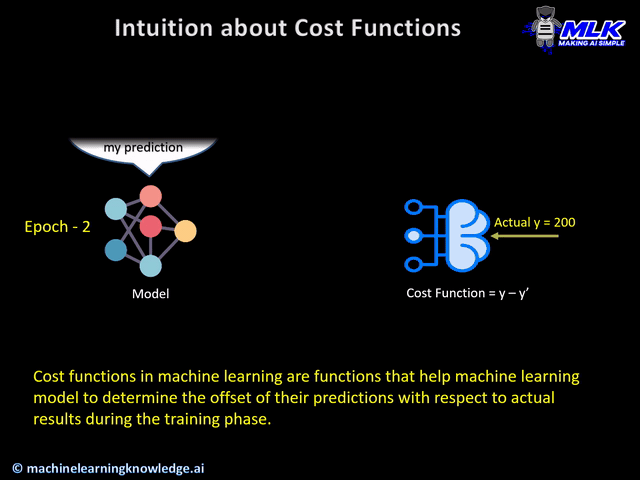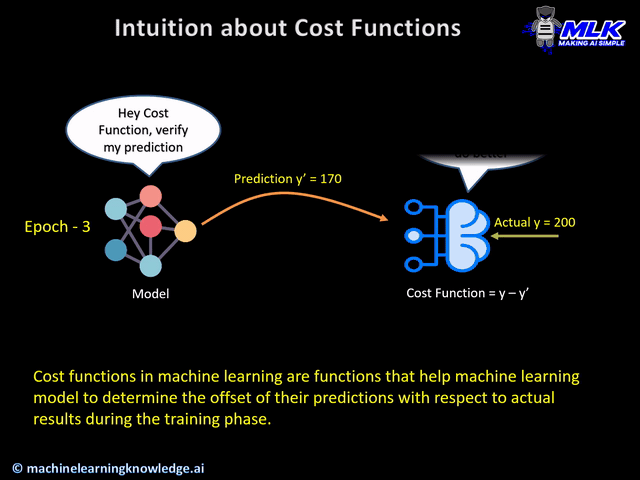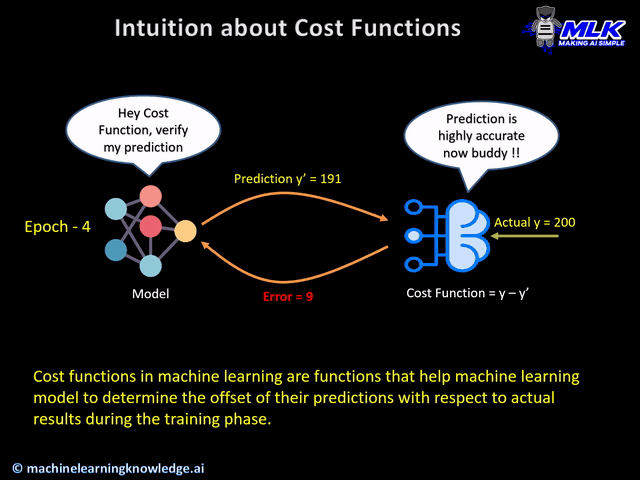
Types of PyTorch Loss Functions
1. PyTorch Loss Functions for Regression
Let us first see what all loss functions in PyTorch we can use for regression problems.
These regression loss functions are calculated on the basis of residual or error of the actual value and predicted value. The below illustration explains this concept.
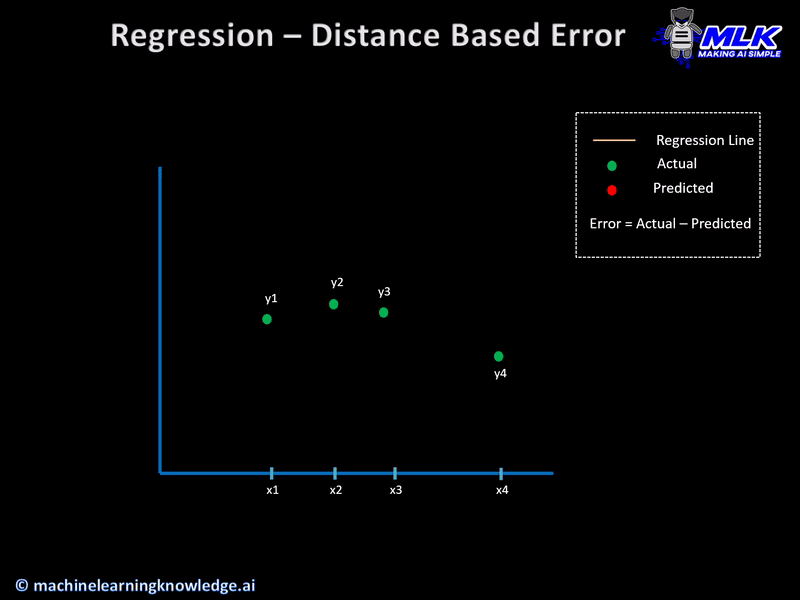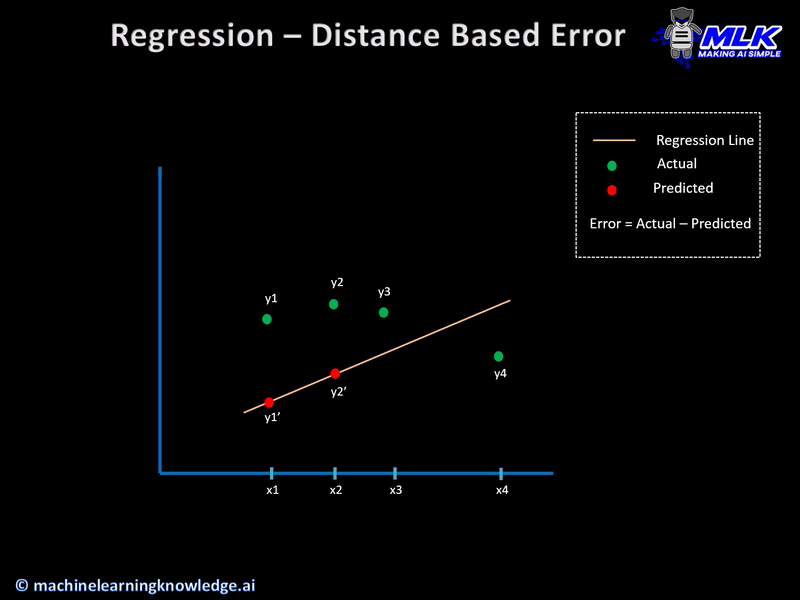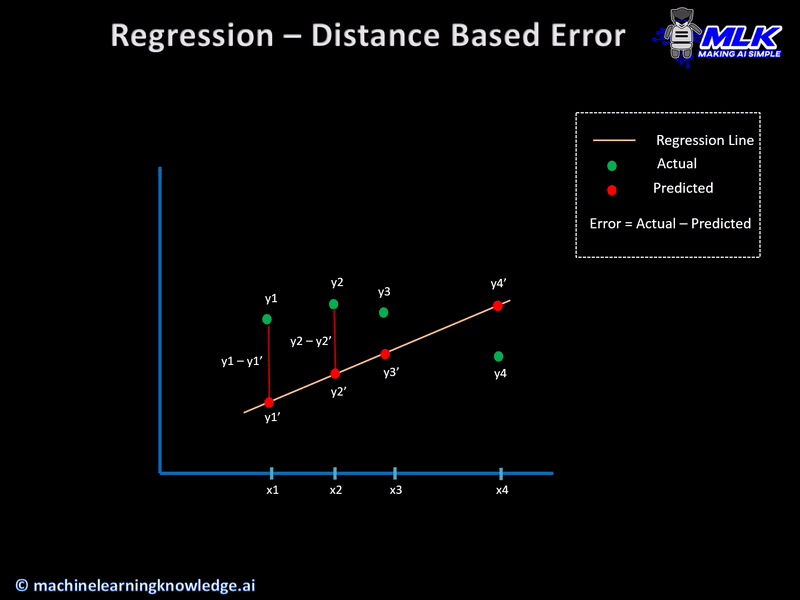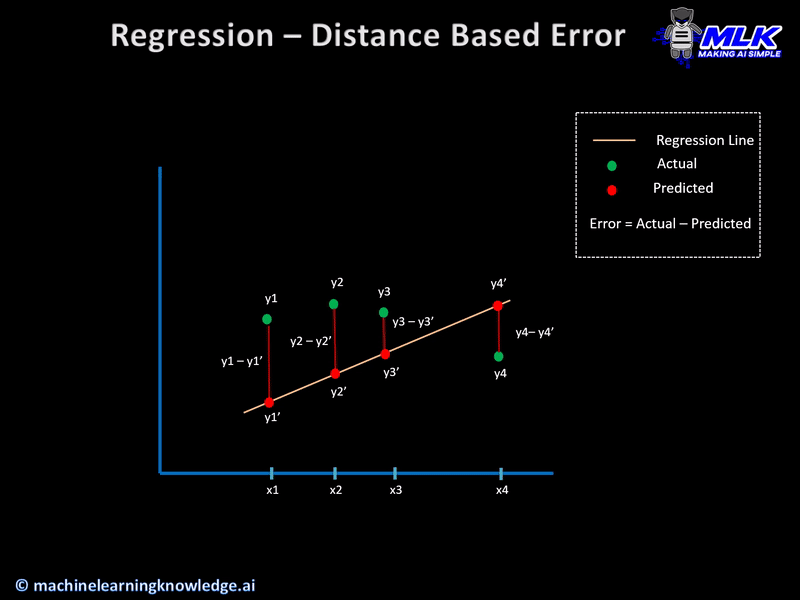
i) Mean Absolute Error
Mean Absolute Error(MAE) or L1 Loss helps in calculating the average of absolute difference within actual values and expected values.
When could it be used?
Mean Absolute Error is used in regression problems, specifically in those cases where target variables contain outliers.
Syntax
Below is the syntax of Mean Absolute Error in PyTorch.
torch.nn.L1LossExample of Mean Absolute Error in PyTorch
The below example shows how we can implement Mean Absolute Error in PyTorch.
import torch
import torch.nn as nn
input = torch.randn(4, 6, requires_grad=True)
target = torch.randn(4, 6)
mae_loss = nn.L1Loss()
output = mae_loss(input, target)
output.backward()
print('input: ', input)
print('target: ', target)
print('output: ', output)
input: tensor([[-1.1755, 1.5283, -0.7174, -1.3634, -0.3620, -1.2202],
[-0.1568, 0.2724, 0.8901, -0.8379, -0.3100, -0.4176],
[ 0.4500, 0.8241, 0.5357, 0.4286, 1.9292, -2.2875],
[ 1.4657, -0.6260, 1.0961, 1.7617, -0.7118, 1.3014]],
requires_grad=True)
target: tensor([[ 1.4000, -0.6161, 0.4187, -0.8206, 0.9031, 0.2457],
[ 2.3506, -0.0032, 2.6048, 0.1283, -1.4994, 1.9908],
[ 2.1236, 1.4097, -0.1516, 0.8269, 1.5431, 0.2846],
[ 0.0561, 0.0031, 1.0905, -0.8874, 2.4385, 0.7125]])
output: tensor(1.3720, grad_fn=<L1LossBackward>)
ii) Mean Squared Error Function
The Mean Squared Error is also known as L2 Loss. This loss function helps in calculating the mean of squared differences that occur within actual and expected values.
The output produced by the MSE loss function is always a positive result, irrespective of actual and expected values. For the purpose of improving the model, we should aim to achieve the lowest possible L2 Loss value, a perfect would be closer to 0.0.
When could it be used?
MSE is used for regression problems where there is less noise or outlier in data. Otherwise, since we square the error, the MSE will amplify due to the presence of outliers.
Syntax
Below is the syntax of Mean Square Error in PyTorch.
torch.nn.MSELossExample of Mean Square Error in PyTorch
The below example shows how we can implement Mean Square Error in PyTorch.
input = torch.randn(2, 5, requires_grad=True)
target = torch.randn(2, 5)
mse_loss = nn.MSELoss()
output = mse_loss(input, target)
output.backward()
print('input: ', input)
print('target: ', target)
print('output: ', output)
input: tensor([[-1.0470, -1.5886, 1.1301, -0.5288, -0.3676],
[-0.2339, 0.6762, 0.5807, 0.2500, -0.7708]], requires_grad=True)
target: tensor([[-0.5139, 0.0780, -0.2450, 0.7559, 1.2605],
[-0.4927, -0.5196, 1.9237, 1.5240, 0.2913]])
output: tensor(1.5305, grad_fn=<MseLossBackward>)
2. PyTorch Loss Functions for Classification
Let us now understand the PyTorch loss functions for classification problem that is generally calculated using probabilistic losses.
i) Negative Log-Likelihood Loss Function
Negative Log-Likelihood Loss Function is used with models that include softmax function performing as output activation layer.
When could it be used?
This loss function is used in the case of multi-classification problems.
Syntax
Below is the syntax of Negative Log-Likelihood Loss in PyTorch.
torch.nn.NLLLoss
Example of Negative Log-Likelihood Loss in PyTorch
The below example shows how we can implement Negative Log-Likelihood Loss in PyTorch.
input = torch.randn(3, 5, requires_grad=True)
# every element in target should have 0 <= value < C
target = torch.tensor([1, 0, 4])
m = nn.LogSoftmax(dim=1)
nll_loss = nn.NLLLoss()
output = nll_loss(m(input), target)
output.backward()
print('input: ', input)
print('target: ', target)
print('output: ', output)
input: tensor([[ 0.2630, 1.6641, 0.4839, -0.1320, 1.2639],
[ 0.5138, -0.5355, 0.7273, 0.7598, 1.5475],
[ 1.0940, 0.1302, 0.0469, 0.7980, 1.1153]], requires_grad=True)
target: tensor([1, 0, 4])
output: tensor(1.3336, grad_fn=<NllLossBackward>)
ii) Cross-Entropy Loss Function
The cross-entropy loss function helps in calculating the difference within two different probability distributions for a set of variables.
With the help of the score calculated by the cross-entropy function, the average difference between actual and expected values is derived.
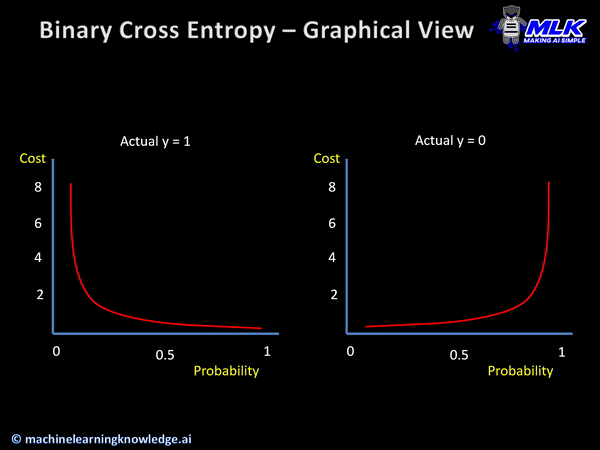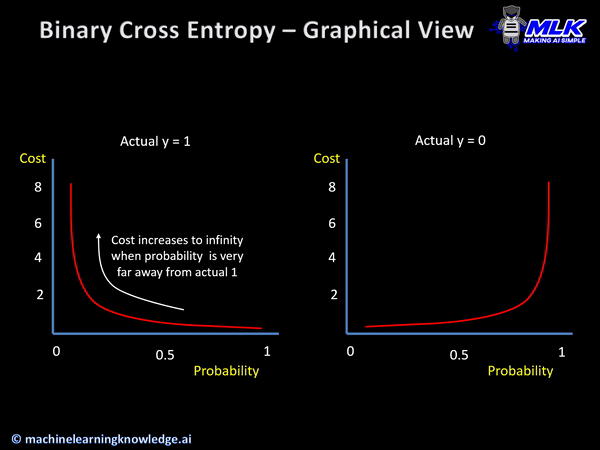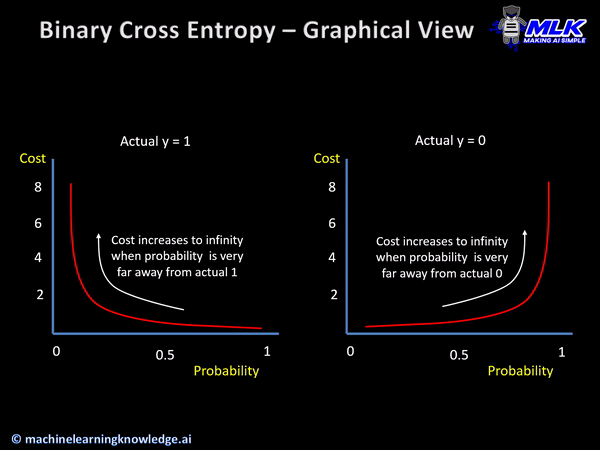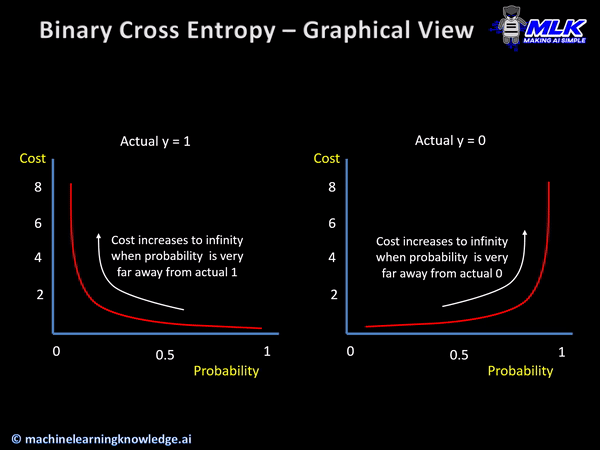
When could it be used?
This function can be used for binary classification.
Syntax
Below is the syntax of the Cross-Entropy loss function in PyTorch.
torch.nn.CrossEntropyExample of Cross-Entropy Loss in PyTorch
The below example shows how we can implement Cross-Entropy Loss in PyTorch.
input = torch.randn(3, 5, requires_grad=True)
target = torch.empty(3, dtype=torch.long).random_(5)
cross_entropy_loss = nn.CrossEntropyLoss()
output = cross_entropy_loss(input, target)
output.backward()
print('input: ', input)
print('target: ', target)
print('output: ', output)
input: tensor([[ 0.1988, -1.1513, -0.6530, -0.5703, 1.2801],
[ 0.6243, -0.2132, -0.4043, -1.3649, 0.9426],
[ 0.9512, -0.6280, 0.6304, 0.4150, -1.1580]], requires_grad=True)
target: tensor([3, 3, 0])
output: tensor(2.1839, grad_fn=<NllLossBackward>)
iii) Hinge Embedding Loss Function
Now we are going to see loss functions in PyTorch that measures the loss given an input tensor x and a label tensor y (containing 1 or -1).
When could it be used?
The hinge embedding loss function is used for classification problems to determine if the inputs are similar or dissimilar.
Syntax
Below is the syntax of the hinge embedding loss function in PyTorch.
torch.nn.HingeEmbeddingLossExample of Hinge Embedding Loss in PyTorch
input = torch.randn(3, 5, requires_grad=True)
target = torch.randn(3, 5)
hinge_loss = nn.HingeEmbeddingLoss()
output = hinge_loss(input, target)
output.backward()
print('input: ', input)
print('target: ', target)
print('output: ', output)
input: tensor([[-0.4524, 1.8945, 1.3809, -0.3340, -0.7647],
[-0.4622, 0.2943, -0.8341, -0.3378, 0.4770],
[-1.1703, -0.2997, 0.6076, -0.4941, 0.9926]], requires_grad=True)
target: tensor([[-0.2517, -0.2383, 0.2874, 1.7514, -1.2939],
[-0.5958, 0.1940, 0.5979, -0.9577, 0.2096],
[-1.0131, 0.4979, 0.3774, -1.3164, 1.8593]])
output: tensor(1.0850, grad_fn=<MeanBackward0>)
Conclusion
This is the end of another PyTorch tutorial that focused on different types of functions in PyTorch. We understood the syntax of these loss functions along with examples and in which scenarios they should be used.
Reference – PyTorch Documentation
